Qu’est-ce que la programmation linéaire ?
Contrairement à ce que pourrait laisser penser son nom, la programmation linéaire n’est pas une nouvelle méthode de programmation consistant à écrire du code sous forme de lignes… (ah c’est déjà ce que l’on fait ?!)
La programmation linéaire est une méthode d’optimisation permettant de déterminer la solution optimale à un problème mathématique formulé avec des équations dites linéaires.
Pour rappel, on appelle fonction linéaire toute fonction pouvant s’écrire sous la forme : \( f(x) = ax + b \)
Certaines opérations sur les fonctions linéaires donnent aussi des fonctions linéaires : somme de 2 fonctions linéaires, multiplication d’une fonction linéaire par une constante...
La formulation d’un problème à résoudre par programmation linéaire est composée :
- d’une fonction objectif linéaire qui est la fonction que l’on veut optimiser en minimisant ou maximisant sa valeur
- de contraintes représentées par des égalités ou inégalités linéaires
- de variables de décision qui sont les inconnues à déterminer et soumises aux contraintes définies
Sous forme mathématique, ça ressemblerait à ça :
\[ \begin{aligned} Max\ (Min) \quad z=& \sum_{j=1}^{n} c_{j} x_{j} \\ \text { s.c. } & \sum_{j=1}^{n} a_{i j} x_{j} \leq b_{i} \quad i \in I \subseteq\{1, \ldots, m\} \\ & \sum_{j=1}^{n} a_{k j} x_{j} \geq b_{k} \quad k \in K \subseteq\{1, \ldots, m\} \\ & \sum_{j=1}^{n} a_{r j} x_{j}=b_{r} \quad r \in R \subseteq\{1, \ldots, m\} \end{aligned} \]
Les ensembles I, K et R sont disjoints et \( I \cup K \cup R = \{1,...,m\} \).
L'abréviation \( \text { s.c. } \) signifie "sous les contraintes".
Ne vous laissez pas déstabiliser par ces formules de maths, tout deviendra plus clair avec un exemple concret. Mais avant...
Dans quels cas la programmation linéaire est-elle utilisée ?
La programmation linéaire est largement utilisée dans la recherche opérationnelle, qui est l'ensemble des méthodes et techniques orientées vers la recherche du meilleur choix dans la façon d'opérer, en vue d'aboutir au résultat visé ou au meilleur résultat possible.
Elle est aussi utilisée dans la gestion d’entreprise pour de la planification, de la production, le transport ou dans la R&D. Bien que les problèmes de gestion modernes soient en constante évolution, la plupart des entreprises cherchent et continueront à chercher à maximiser leurs profits en minimisant les coûts. En utilisant la programmation linéaire, beaucoup de problèmes peuvent être formulés et résolus de manière optimale.
Exemple de problème que l’on peut modéliser et résoudre avec la programmation linéaire
Prenons un exemple simple de problème de maximisation de profit (exemple tiré du cours de Didier Smets).
Un fabricant de voitures propose 2 modèles à la vente, des grosses voitures et des petites voitures. Les grosses voitures sont vendues à 16000 € unité tandis que les petites voitures à 10000 € unité.
Son problème vient de l’approvisionnement limité en deux matières premières, le
caoutchouc et l’acier. La construction d’une petite voiture nécessite l’emploi d’une unité de caoutchouc et d’une unité d’acier, tandis que celle d’une grosse voiture nécessite une unité de caoutchouc mais deux unités d’acier.
Dans son stock, il ne lui reste plus que 400 unités de caoutchouc et 600 unités d’acier.
Il aimerait savoir combien de petites et de grosses voitures il doit produire afin de maximiser son chiffre d'affaires en prenant en compte son stock actuel.
Nous appellerons x le nombre de grosses voitures produites, y le nombre de petites voitures produites, et z le chiffre d'affaires résultant. Le problème se traduit alors sous la forme:
\[ \begin{aligned} \text{maximiser} \quad &z=16000x+10000 y \\ \text { s.c. } & x+y \leq 400 \\ & 2 x+y \leq 600 \\ & x \geq 0, y \geq 0 \end{aligned} \]
Explication :
Nous souhaitons maximiser le chiffre d’affaires z qui est égal à 16000 * le nombre de grosses voitures vendues + 10000 * le nombre de petites voitures vendues.
Les contraintes sont telles que :
- Le nombre d’unités de caoutchouc utilisées (
x + ycar il faut 1 unité de caoutchouc pour chaque voiture) ne peut excéder 400 - Le nombre d’unités d’acier utilisées (
2x + ycar il faut 2 unités d’acier pour chaque grosse voiture et 1 unité pour chaque petite voiture) ne peut excéder 600 - Le nombre de petites/grosses voitures produites est positif
En représentation graphique nous aurions ce graphe-là avec la partie rayée qui représente l’ensemble des solution possibles.
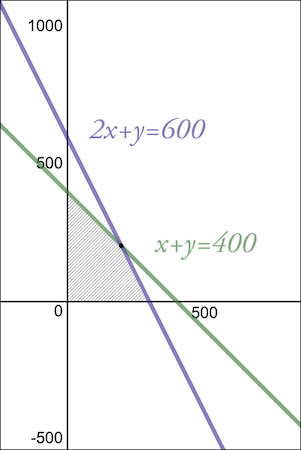
Essayons de résoudre ce problème en Python.
Résolution du problème en Python en utilisant PuLP
PuLP est une bibliothèque open source pour la programmation linéaire en Python. Elle met à disposition tous les outils pour modéliser un problème et les résoudre en faisant appel à différents types de solveurs standards utilisant des algorithmes de résolution différents. C'est en fait un wrapper qui permet la formulation du problème en Python.
Reprenons l’exemple précédent dont la formulation est la suivante :
\[ \begin{aligned} \text{maximiser} \quad &z=16000x+10000 y \\ \text { s.c. } & x+y \leq 400 \\ & 2 x+y \leq 600 \\ & x \geq 0, y \geq 0 \end{aligned} \]
Nos variables de décisions sont x et y. Elles doivent être des valeurs entières positives.
# Nombre de grosses voitures produites
x = LpVariable('x', lowBound=0, cat=LpInteger)
# Nombre de petites voitures produites
y = LpVariable('y', lowBound=0, cat=LpInteger)
Initialisons le problème pour pouvoir lui ajouter nos contraintes et fonction objectif. Nous voulons maximiser notre fonction objectif donc nous utilisons LpMaximize (LpMinimize si l’on veut minimiser).
probleme = LpProblem(name='chiffre_affaires', sense=LpMaximize)
Ajoutons à notre problème les contraintes par rapport au stock :
eest l’expression à comparer et contient généralement les variables de décision que nous avons défini plus hautsenseest le sens de l’inégalité avecLpConstraintLEpour “less equal” etLpConstraintGEpour “greater equal”- Le nom de la contrainte peut servir pour débugger le problème, si nous souhaitons afficher les contraintes non utilisées par exemple
rhs(right hand-side) est la constante à laquelle l’expression est comparée
contrainte_caoutchouc = LpConstraint(e=x + y, sense=LpConstraintLE, name='contrainte_caoutchouc', rhs=n_caoutchouc)
probleme.add(contrainte_caoutchouc)
contrainte_acier = LpConstraint(e=2 * x + y, sense=LpConstraintLE, name='contrainte_acier', rhs=n_acier)
probleme.add(contrainte_acier)
Nous pouvons aussi les ajouter de la manière suivante car PuLP reconnaît le type d’expression passée (contrainte vs fonction objectif).
probleme += (x+y <= n_caoutchouc)
probleme += (2*x+y <= n_acier)
Ajoutons ensuite la fonction objectif à maximiser au problème.
fonction_objectif = LpAffineExpression(e=prix_grosse_voiture*x + prix_petite_voiture*y)
probleme.setObjective(fonction_objectif)
Ou simplement
probleme += prix_grosse_voiture*x + prix_petite_voiture*y
Enfin, initialisons le solveur à utiliser. Ici nous utilisons CBC (qui est aussi le solveur par défaut si aucun solveur n’est spécifié) avec un temps d’exécution maximum de 20 secondes. Vous pouvez retrouver la liste des solveurs disponibles ainsi que leurs options ici.
solver = PULP_CBC_CMD(timeLimit=20, msg=True)
probleme.solve(solver=solver)
Une fois que le problème a été résolu (moins d'un centième de secondes ici), nous pouvons afficher les valeurs trouvées.
print(f'x = {x.value()}')
print(f'y = {y.value()}')
Ce qui nous donne le résultat suivant :
x = 200.0
y = 200.0
Le fabricant devra donc fabriquer 200 petites et grosses voitures pour maximiser son chiffre d’affaires.
Vous trouverez ici le programme complet si vous souhaitez essayer en local pour voir comment évolue la solution optimale en fonction des paramètres d’entrée.
Comment débugger ?
Plus il y a d’éléments à prendre en compte, plus il y a de contraintes et plus le solveur met du temps à trouver une solution optimale. Dans certains cas, le solveur ne trouve pas de solution optimale. Le résultat de l’optimisation peut avoir ces statuts-là :
- Optimal : la solution optimale a été trouvée
- Not Solved : statut par défaut du problème avant qu’il ne soit résolu
- Infeasible : il n’existe pas de solution pour le problème
- Unbounded : la fonction objectif est non limitée (ne peut pas atteindre un min ou un max)
- Undefined : la solution n’a pas été trouvée (mais elle peut exister)
Pour obtenir le statut de l’optimisation, il suffit d’afficher cet attribut :
probleme.status
Si le flag msg a été mis à True au niveau du solveur, des logs vont être affichés lors de la résolution et peuvent aider à déterminer pourquoi le programme plante ou fournit un résultat différent de celui que l’on attend.
At line 2 NAME MODEL
At line 3 ROWS
At line 7 COLUMNS
At line 18 RHS
At line 21 BOUNDS
At line 24 ENDATA
Problem MODEL has 2 rows, 2 columns and 4 elements
Coin0008I MODEL read with 0 errors
...
Result - Optimal solution found
Objective value: 5200000.00000000
Enumerated nodes: 0
Total iterations: 0
Time (CPU seconds): 0.00
Time (Wallclock seconds): 0.00
Option for printingOptions changed from normal to all
Total time (CPU seconds): 0.00 (Wallclock seconds): 0.00
Conclusion
Dans cet article, je vous ai fait une présentation rapide de la programmation linéaire et montré un exemple très simple de ce qu’il est possible de faire avec mais nous pouvons résoudre des problèmes beaucoup plus compliqués. Généralement, trouver une formulation linéaire du problème est la partie compliquée du processus. Nous avons aussi utilisé très peu d’options de PuLP dans ce code d’exemple mais il y a énormément de personnalisation possible au niveau solveur, et plusieurs fonctions qui permettent de débugger le code (se réferer à la documentation https://coin-or.github.io/pulp/index.html).
Il existe d’autres bibliothèques pour la programmation linéaire comme ORTools de Google. Dans le cadre de ma mission, j’ai eu l’occasion de l’essayer et je trouve personnellement que PuLP est plus simple à prendre en main.
Aujourd’hui, la programmation linéaire est enseignée dans de nombreuses universités et il existe de nombreux supports de cours disponibles si vous souhaitez en savoir plus dessus.