Imaginez que vous êtes dans un train, à destination des vacances.
Comme d'habitude, vous décidez d'aller vers Bayonne pour ces vacances (pour des raisons tout à fait liées au soleil). Vous prenez chaque année le même train qui part de votre gare préférée à la même heure et qui arrive à la même heure sur place, pour être sûr de profiter de la façon la plus optimale de l'ambiance. Tout va bien...
Du côté de la SNCF, tout est prêt : de jeunes saisonniers ont été recrutés aux postes d'aiguillage des voies pour qu'ils les opèrent manuellement afin de diriger les trains vers le droit chemin.

Le petit problème est qu'ils n'ont aucun moyen de savoir dans quelle direction doit partir le train, comme ils n’ont pas eu le temps de récupérer le planning de la journée. Pas de problème, comme il y a des radios, il suffit alors de contacter les conducteurs de train lorsqu'ils approchent !
Et ce jour-ci, c'était un petit nouveau qui faisait son premier jour depuis 6 heures du matin. Tous les trains qui sont passés par lui sont partis sur la voie de droite après qu'il les ait contactés, et ce jusqu'à midi... Dans un souci de fluidité, d'optimisation (ou de flemme et/ou de fatigue), il décidait d'anticiper que tous les trains de la journée allaient à droite.
Votre train, parti à 14 heures de la gare, arrive à 16 heures à proximité de la jonction, mais soudain s'arrête... Et fait marche arrière... Mais pourquoi ?!
Le petit jeune venait de faire une erreur. Votre train devait partir à gauche, mais a laissé la jonction vers la droite... Et s'ensuit un retard de 45 minutes qui ruine tous vos plans, une énorme vague d'énervement dans le train, entre les passagers, le conducteur et vous qui blâmez l'incompétence de la personne chargée d'aiguiller le train. Ce dernier pensait que tous les trains iraient à droite par habitude, mais le vôtre ne répondait pas à cette tendance.
Vous êtes une victime de la SNCF prédiction de branche.
Comment ça marche dans les processeurs ?
L'exemple ci-dessus est un peu tiré par les cheveux, mais résume bien ce que la prédiction de branchement vise à faire : à anticiper le résultat d'un branchement pour fluidifier, optimiser l'exécution d'un programme, d'un algorithme.
Quelques généralités
Tous les ordinateurs qui nous entourent possèdent un processeur, qui se charge d'exécuter une série d'instructions (provenant du code d'un programme) afin d'en fournir le résultat après leur exécution.
Ces instructions passent dans le pipeline d'instructions du processeur, qui va traiter chaque instruction lors de ses cycles d'horloge via plusieurs étapes (ici, la version simplifiée en 5 étapes) :
- Il récupère l'instruction qui était jusqu'à présent en attente ;
- Il décode l'instruction, i.e. il va identifier quelle est l'instruction qu'il vient de récupérer ;
- Il exécute l'instruction ;
- S'il a besoin d'accéder à quelque chose dans la mémoire pour l'instruction, il le fait maintenant ;
- Il écrit le résultat de l'exécution dans ses registres en interne.
Dès qu'une de ces étapes est terminée pour une instruction, elle est lancée pour une autre : si l'instruction A a été récupérée, elle passe à l'étape de décodage, et une instruction B passe par l'étape de récupération, ainsi de suite.
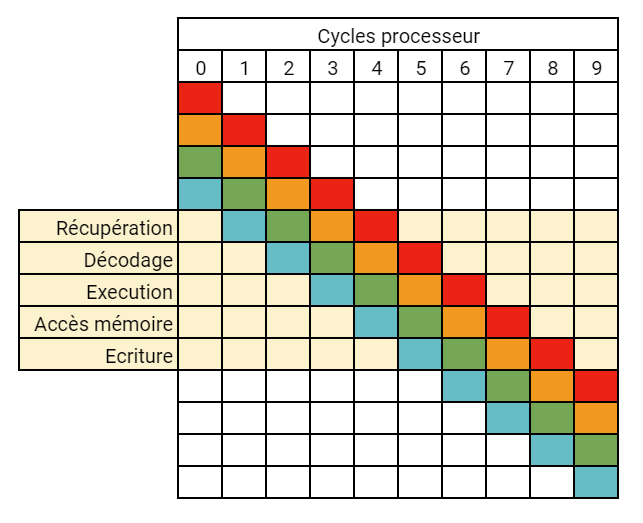
Les instructions sont notamment chargées séquentiellement dans le pipeline du processeur. Ceci peut poser des soucis lorsque le programme peut avoir plusieurs comportements en fonction de l'état interne de ses variables (avec un if, par exemple) - on parle de branches.
La prédiction de branche et l'exécution spéculative
Lorsqu'un programme possède des branches, c'est-à-dire différentes possibilités de progression en fonction des valeurs d'entrée, l'exécution des instructions n'est plus faite de façon séquentielle.
En effet, prenons un code simple (ici en C) :
#include <stdio.h>
void main(int i) {
if (i > 10) {
printf("i > 10!");
} else {
printf("i <= 10!");
}
}
Il est très très simple (le Hello, world! du if), mais contient malgré tout deux branches qui dépendent de l'entrée (ici, la valeur de i) et du résultat de la comparaison, ce qui rend l'exécution non-linéaire : soit il doit exécuter la première branche (i > 10) puis ignorer les instructions qui constituent la deuxième branche (le processeur les considère comme des NOP, des no-operations, des instructions qui ne font rien), soit les instructions de la première branche sont considérées comme des NOP jusqu'à atteindre la deuxième branche.
Le deuxième cas serait le plus défavorable ici, comme cela implique qu'il a quand même lu ce qu'étaient les instructions de la première branche avant de se rendre compte que "non, je ne dois pas les exécuter"... Ce qui constitue une perte de temps pour le processeur.
(Ceci est négligeable dans un tel exemple, mais l’exemple est présent pour l'explication basique.)
C'est pour ça qu'il existe dans les processeurs un mécanisme qui permet de tenter de "deviner" quelle branche va être prise : c'est le titre de cette sous-partie, la prédiction de branche (branch prediction) !
Avec ça, le processeur va "parier" sur le fait qu'il doit aller sur telle ou telle branche en fonction de ce qui s'est passé avant (et donc charger les instructions correspondant à la branche choisie), avant même d'arriver sur les instructions où se situe le branchement.
A la suite de ce pari, le processeur va charger en avance — c’est-à-dire avant que le programme ne soit arrivé à ce point-là — les instructions qui correspondent à la branche sur laquelle il a parié et va les mettre dans son pipeline, prêtes à être exécutées dès que les entrées sont prêtes.
Si son pari est réussi, il aura évité de charger des instructions inutiles et aura gagné du temps. Mais si son pari échoue, il aura chargé des instructions inutiles, auquel cas il doit les purger de son pipeline pour aller récupérer les bonnes instructions à exécuter.
Cela va donc de paire avec l'exécution spéculative (speculative execution) : suite au pari que le processeur a fait sur quelles instructions vont lui servir, il va commencer à les exécuter avant que le programme ait normalement avancé à ce stade-là. De fait, il réordonne l'ordre des instructions pour que celles de la branche qu'il a favorisée s'exécutent plus tôt qu'initialement prévu par le programme : cela s'appelle l'exécution dans le désordre (out-of-order execution). Les implications sont les mêmes : s'il a réussi, il aura gagné du temps, sinon il en aura perdu à devoir tout recommencer et tout réordonner.
A quel point ça nous impacte ?
On ne se rend pas nécessairement compte de son efficacité au quotidien, il est vrai. Mais il a un véritable impact sur les performances d'un algorithme dans lequel, par exemple, on répète une succession d'opérations sur un ensemble de données.
Le travail sur des données triées versus des données non triées est un exemple parfait pour ça.
Le code qui suit, en C, en est un exemple :
Ce code va remplir un tableau de 65 536 entrées avec des valeurs aléatoires (entre 0 et 32 767). Pour chaque valeur, selon qu'elle soit inférieure ou supérieure à 16 383, il va exécuter une certaine suite d'opérations (très simples ici, en O(1)). On répète cela 100 000 fois et on mesure le temps passé pour le faire.
Le #ifdef permet juste de dire qu'on veut compiler le programme en ajoutant la ligne permettant de trier le tableau avant le traitement ou non, et la fonction compare(const void*, const void*) sert juste de fonction de comparaison pour le tri.
#include <stdlib.h>
#include <time.h>
#include <stdio.h>
unsigned long ARRAY_SIZE = 65536;
unsigned long OP_REPEAT = 100000;
#ifdef SORT_TEST
int compare(const void *first_element, const void *second_element)
{
uint first_int = *((uint *)first_element);
uint second_int = *((uint *)second_element);
if (first_int > second_int)
return 1;
if (first_int < second_int)
return -1;
return 0;
}
#endif
void main()
{
uint number_array[ARRAY_SIZE];
unsigned long low_numbers = 0;
unsigned long high_numbers = 0;
unsigned long low_numbers_sum = 0;
unsigned long high_numbers_sum = 0;
for (uint i = 0; i < ARRAY_SIZE; i++)
{
number_array[i] = rand();
}
#ifdef SORT_TEST
qsort(number_array, sizeof(number_array) / sizeof(*number_array), sizeof(*number_array), compare);
#endif
srand(time(NULL));
clock_t begin_time = clock();
for (uint k = 0; k < OP_REPEAT; k++)
{
for (uint j = 0; j < ARRAY_SIZE; j++)
{
if (number_array[j] < ((uint) RAND_MAX) >> 1) // RAND_MAX = 32767 ici, dans stdlib.h
{
low_numbers++;
low_numbers_sum += number_array[j];
}
else
{
high_numbers++;
high_numbers_sum += number_array[j];
}
}
}
clock_t end_time = clock();
double time_taken = (double)(end_time - begin_time) * 1000 / CLOCKS_PER_SEC;
printf("Number of low numbers: %ld\n", low_numbers);
printf("Number of high numbers: %ld\n", high_numbers);
printf("Time taken: %lf ms\n", time_taken);
}
Mais est-ce qu’un simple tri permet d’arranger la situation ?
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ gcc -o sample ./sample.c -O2
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ time ./sample
Number of low numbers: 3280000000
Number of high numbers: 3273600000
Time taken: 20207.138000 ms
real 0m20.212s
user 0m20.209s
sys 0m0.000s
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ gcc -o sample ./sample.c -O2 -D SORT_TEST
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ time ./sample
Number of low numbers: 3266100000
Number of high numbers: 3287500000
Time taken: 3764.451000 ms
real 0m3.768s
user 0m3.766s
sys 0m0.000s
Le premier résultat correspond à l’exécution du programme sans le tri, le second avec. Et on se rend compte qu'avec les données triées, cela a pris 5 fois moins de temps que sur les données non triées...
Et ce comportement n'est pas propre au langage choisi ici. Avec le même exemple, mais en Java, les résultats sont similaires :
import java.util.Arrays;
import java.util.Random;
import java.util.concurrent.TimeUnit;
public class Main {
private final static int ARRAY_SIZE = 65536;
private final static int OP_NUMBER = 100000;
private final static int RAND_RANGE = 32767;
public static void main(String[] args) {
int[] numberArray = new int[ARRAY_SIZE];
long lowNumbers = 0;
long highNumbers = 0;
long lowNumbersSum = 0;
long highNumbersSum = 0;
for (int i = 0; i < ARRAY_SIZE; i++) {
numberArray[i] = new Random().nextInt(RAND_RANGE);
}
if (args.length > 0) {
Arrays.sort(numberArray);
}
long start = System.nanoTime();
for (int j = 0; j < OP_NUMBER; j++) {
for (int k = 0; k < ARRAY_SIZE; k++) {
if (numberArray[k] < RAND_RANGE / 2) {
lowNumbers++;
lowNumbersSum += numberArray[k];
} else {
highNumbers++;
highNumbersSum += numberArray[k];
}
}
}
long end = System.nanoTime();
System.out.println(String.format("Number of low numbers: %d", lowNumbers));
System.out.println(String.format("Number of high numbers: %d", highNumbers));
System.out.println(String.format("Time taken: %s seconds.", (double) (TimeUnit.NANOSECONDS.toMillis(end - start) / 1000)));
}
}
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/untitled/out/production$ java -classpath ./** com.ippon.company.Main
Number of low numbers: 3283400000
Number of high numbers: 3270200000
Time taken: 23.0 seconds.
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/untitled/out/production$ java -classpath ./** com.ippon.company.Main "sort"
Number of low numbers: 3297900000
Number of high numbers: 3255700000
Time taken: 7.0 seconds.
Ici, le facteur n'est que de 3* environ, mais cela reste significatif.
* Il est important de noter que Java fait de la compilation just-in-time (détaillé un peu plus bas), ce qui rend les premières exécutions plus lentes que les suivantes. De fait, les résultats ici sont biaisés car on relance la JVM à chaque fois. Si cet algorithme était lancé plusieurs fois dans la même JVM, avec le tri, le temps d’exécution descend à 3 secondes en moyenne. Ceci est plus rapide que le code en C avec la compilation en -O2, car Java a optimisé plus agressivement que GCC ici. En utilisant le flag -O3 pour le code en C, celui-ci reprend la tête, bien que de peu.
La question est donc : pourquoi tant de différences entre les deux ?
La réponse est dans ce qui est décrit avant !
Pour cet exemple, sur un tableau trié, le processeur peut aisément spéculer sur le fait que pendant un certain temps, toutes les valeurs seront inférieures à 16383, et du coup va exécuter en avance de phase la première branche correspondante.
Au moment où les valeurs dépassent cette limite, il va se tromper un peu au début (le temps de perdre son habitude et de commencer à exécuter l'autre branche de façon anticipée), mais le comportement revient vite à la normale, c'est-à-dire qu'il va correctement prédire dans quelle branche il devra aller et va la charger en amont. Sur un tableau non-trié, il a cependant 50% de chances de se tromper si le tableau est uniformément aléatoire, d'où le temps d'exécution plus long : quand il se trompe, il est obligé de se débarrasser du résultat calculé par erreur, de retrouver les instructions correspondant à la bonne branche et relancer le calcul dessus, ce qui retarde le passage au tour de boucle suivant.
Comment en profiter au maximum ?
Il n'y a pas nécessairement de formule magique pour en profiter (ou plutôt, pour limiter ses dégâts quand il se trompe), si ce n'est réfléchir à quelques points en amont lors de la conception et l'écriture du code :
Est-ce que j'ai le contrôle sur l'entrée ?
C'est-à-dire : est-ce que je peux faire en sorte que l'entrée soit prédictible pour aider les prédictions à aller dans le bon sens (du tri, par exemple, comme avant) ?
Ce n'est pas nécessairement possible, que ça soit par des contraintes au niveau des données, ou que les "contrôler" impliquerait de fait une perte de performances par rapport à ce qu'il y a actuellement — pour rappel, par exemple, le quicksort utilisé en C a une complexité en temps moyenne en O(n log n), et peut ne pas valoir le coup en fonction de ce qui suit.
Est-ce que je connais les résultats attendus ?
Cela consiste à savoir en avance, en tant que développeur, si la fonction/méthode que l'on écrit va passer plus fréquemment par une branche du code qu'une autre.
Dans ce cas, il est possible de réécrire certaines méthodes de sorte à ce que l'on ait des branches en moins — voire plus aucune — pour éviter les erreurs de prédiction. Cela peut se faire en assurant au processeur qu'il ne travaille pas sur des données a priori aléatoires (par exemple en lui garantissant qu'il ait un traitement à faire sur toutes les données qu'il a en entrée, ensuite qu'il a à faire un traitement spécifique sur les données un peu différentes).
Est-ce que je peux l'écrire sans branches (branchless programming) ?
Potentiellement la meilleure option (pour des questions à la fois de performances et parfois, de lisibilité) : s'affranchir des branches complètement.
Parfois, on se rend compte qu'on peut écrire des algorithmes différemment, que ce soit avec le recul, ou avec une idée lumineuse, ou juste de l'expérience en plus, et ça permet de se rendre compte parfois que certains morceaux de code n'ont pas lieu d'être — les if sont des bons exemples dans le cadre des prédictions de branches. Et que même, de façon générale, la première approche — l'approche "naïve" — n'est pas forcément la meilleure.
Par exemple, le code précédent peut être un peu optimisé de la sorte en remplaçant les if par des... maths !
for (uint k = 0; k < OP_REPEAT; k++)
{
for (uint j = 0; j < ARRAY_SIZE; j++)
{
uint tmp = number_array[j] / ((uint)RAND_MAX >> 1);
low_numbers += (uint)1 - tmp;
low_numbers_sum += (uint)(1 - tmp) * number_array[j];
high_numbers += tmp;
high_numbers_sum += tmp * number_array[j];
}
}
En refaisant le test avec ce code-là, on se rend compte que le code n'est plus dépendant du tri et de fait, des branches :
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ gcc -o sample ./sample.c -O2
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ ./sample
Number of low numbers: 3266000000
Number of high numbers: 3287600000
Time taken: 5763.214000 ms
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ gcc -o sample ./sample.c -O2 -D SORT_TEST
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ ./sample
Number of low numbers: 3301100000
Number of high numbers: 3252500000
Time taken: 5770.174000 ms
... Mais qu'il n'est pas encore optimisé au maximum, comme on ne retrouve pas exactement les résultats d'avant avec branche et tri. Mais c'est déjà une bonne piste, comme le temps d'exécution est du coup constant !
Cependant, il s'agit aussi de trouver la bonne balance entre optimisation et compréhension. Le code optimisé ici est bien plus complexe à lire avec cela qu'avec les ifs. Un choix est donc à faire entre lisibilité et performances.
Une dernière chose à considérer : les compilateurs parviennent parfois à optimiser suffisamment le code à la compilation — qu’elle soit anticipée (AoT, ahead-of-time) ou à la volée (JIT, just-in-time) — de sorte à ce que même s’il y a des branches apparentes dans votre code (if, goto…), les performances seront meilleures que sans. Les compilateurs savent généralement (99.9% des cas) comment faire en sorte que le code s’exécute de la meilleure façon, et il s’agit généralement de cas assez exceptionnels lorsqu’il faut que vous le fassiez à la main.
Ce PDF résume bien la situation à ce sujet : si vous voyez une optimisation possible, il faut la tester. Si les gains justifient la lisibilité du code, alors allez-y, sinon ce n’est pas forcément la peine.
Quelques limitations...
Compilé vs. interprété
Vous avez pu remarquer que les exemples présentés utilisent des langages qui ont un point commun entre eux (j'aurais pu aussi le faire en C# par exemple) : ce sont tous les langages compilés*.
* Petites nuances entre le C et les autres : C compile directement vers du langage machine, le C# et Java sont compilés en des langages intermédiaires (bytecode) que leurs VM exécutent.
Les développeurs sur des langages compilés dépendent notamment du compilateur pour savoir "est-ce qu'il va bien traduire ce que j'ai écrit et potentiellement l'optimiser". Sachant qu'une compilation est, grosso modo, une traduction de A vers B avec quelques étapes supplémentaires (il va d'abord lire tout le code source, rechercher les optimisations, puis traduire), la tâche incombe au développeur de montrer ses intentions du mieux qu'il peut pour éviter certains problèmes après la compilation.
Pour les langages interprétés cependant... Il peut aussi y avoir des soucis.
Ceux-ci, pour s'exécuter, se basent sur un interpréteur (d'où le nom, vraiment), qui est une couche d'abstraction supplémentaire pour l'exécution d'un programme. Et une différence majeure est qu'il exécute à la volée et ligne par ligne le code qu'il lit. Il n'y a pas d'optimisation qui est faite à la volée ici hormis certains cas particuliers, mais de façon générale, il ne peut pas anticiper la suite du programme lorsqu'il interprète et exécute le code.
Cela ajoute de fait du "bruit" dans ce que le processeur va recevoir comme instructions et il se peut, de fait, qu'il ne fasse pas de prédiction de branche pour votre programme alors qu'il pourrait en faire.
L'exemple ici, en Python :
import time
import random
import sys
import array as arr
ARRAY_SIZE = 65536
OP_NUMBER = 1000
RAND_RANGE = int(0x7fff)
number_array = arr.array('i', [])
low_numbers = 0
high_numbers = 0
low_numbers_sum = 0
high_numbers_sum = 0
for i in range(ARRAY_SIZE):
number_array.insert(i, int(random.random() * RAND_RANGE))
if (len(sys.argv) > 1):
number_array = sorted(number_array)
start_time = time.time()
for j in range(OP_NUMBER):
for k in range(ARRAY_SIZE):
if number_array[k] < RAND_RANGE / 2:
low_numbers += 1
low_numbers_sum += number_array[k]
else:
high_numbers += 1
high_numbers_sum += number_array[k]
print(f"Number of low numbers: {low_numbers}")
print(f"Number of high numbers: {high_numbers}")
print(f"--- {time.time() - start_time} seconds ---")
Et après tests, on se rend compte que les temps sont stables ici :
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ python3 sample.py "sort"
Sorting
Number of low numbers: 32905000
Number of high numbers: 32631000
--- 11.255894184112549 seconds ---
ctest@DESKTOP-436J991:/mnt/c/Users/ctest/Desktop$ python3 sample.py
Number of low numbers: 32833000
Number of high numbers: 32703000
--- 12.036502599716187 seconds ---
Du coup, on peut supposer que l'interpréteur ajoute quelque chose de supplémentaire à la lecture du code qui fait qu'il arrive à "s'affranchir" de la contrainte qu'on avait eue avec les langages compilés.
Cela a un coût ceci dit : un temps d'exécution plus long !
Contrairement aux langages compilés testés avant où on répétait l'opération 100 000 fois, ici elle n'est répétée que 1 000 fois pour une durée comparable. Dû à la lourdeur de l'interprétation qui engendre un plus forte consommation de mémoire et ressources CPU (de l'overhead), on est obligé de rabaisser nos prétentions pour garder un temps d'exécution correct.
L'important à retenir est qu'il faut savoir choisir le bon outil pour les bonnes raisons, et surtout bien l'utiliser pour en tirer le meilleur parti. Chaque langage a son lot de subtilités et d'élégance qui font leur charme : savoir ce qu'ils apportent et que chaque ligne écrite peut influencer du tout au tout le résultat fait le charme de la programmation et du développement d'applications ! :)
Possibles abus (vulnérabilités)
En parlant de bien utiliser les outils pour en tirer le meilleur parti, ceux-ci ont, comme tout, des failles...
Et deux* d'entre elles, apparues entre 2017 et 2018, exploitent les principes de l'exécution spéculative et de la prédiction de branchement telles qu'implémentées dans les processeurs : Spectre et Meltdown.
* Il y a plusieurs versions de ces vulnérabilités, ainsi que d'autres vulnérabilités différentes de celles-ci, mais qui se basent sur ces principes pour exister, entre autres.
D'une façon simplifiée, ces failles exploitent ces deux principes pour pousser le processeur à exécuter de façon spéculative des instructions mettant en jeu des données protégées, donc potentiellement des mots de passe, logins, mails, etc... Le lien ci-dessus offre plus de détails à ce sujet.
Ces failles étaient particulièrement terrifiantes vu que pour les corriger définitivement, il fallait que les fabricants de processeurs (AMD et Intel principalement, pour ne pas les citer — certains processeurs ARM qui sont dans nos téléphones sont cependant aussi vulnérables) révisent leurs architectures processeurs. Des patches software avaient été fournis par Microsoft et Unix pour limiter la casse au moment où ces vulnérabilités avaient été dévoilées, mais :
- Comme il s'agit d'une faille au niveau hardware, rien n'empêche qu'elles ne réapparaissent dans le futur ;
- Il y a eu des pertes de performances suite à ces patches (assez conséquentes aux premiers patches, bien moindres maintenant, voir cet article en 2019) — ce qui montre la dépendance vis-à-vis de l'exécution spéculative et de la prédiction de branches pour les performances.
Maintenant, les processeurs depuis 2019 ont implémenté des mesures hardware pour éviter ce genre de failles, mais on ne sait jamais... L'innovation va dans tous les sens, après tout !
Le petit mot de la fin
Sous des noms compliqués se cachent des pièces, invisibles dans la vie de tous les jours, mais maîtresses dans le fonctionnement de nos ordinateurs et des applications que l'on utilise.
La prédiction de branche et l'exécution spéculative ont des bienfaits non-négligeables pour aider à la vitesse d'exécution de nos applications, mais peuvent très vite se retourner contre nous si on ne fait pas attention à la façon dont nous les implémentons.
On utilise très souvent des outils de haut-niveau pour interagir avec les composants de bas-niveau, et savoir comment ces derniers fonctionnent peut nous éclairer, nous aider ou nous donner de bonnes idées pour mieux utiliser ces outils ! Dans le futur, j’essaierai d’explorer d’autres aspects potentiellement méconnus mais qui ont leur importance.


